Polinomial
Fadillah
XI MIPA 6
Pengertian
Dalam dunia matematika, polinomial atau suku banyak adalah pernyataan matematis yang berhubungan dengan jumlahan perkalian pangkat dalam satu atau lebih variabel dengan koefisien.
Bentuk Umum Polinomial
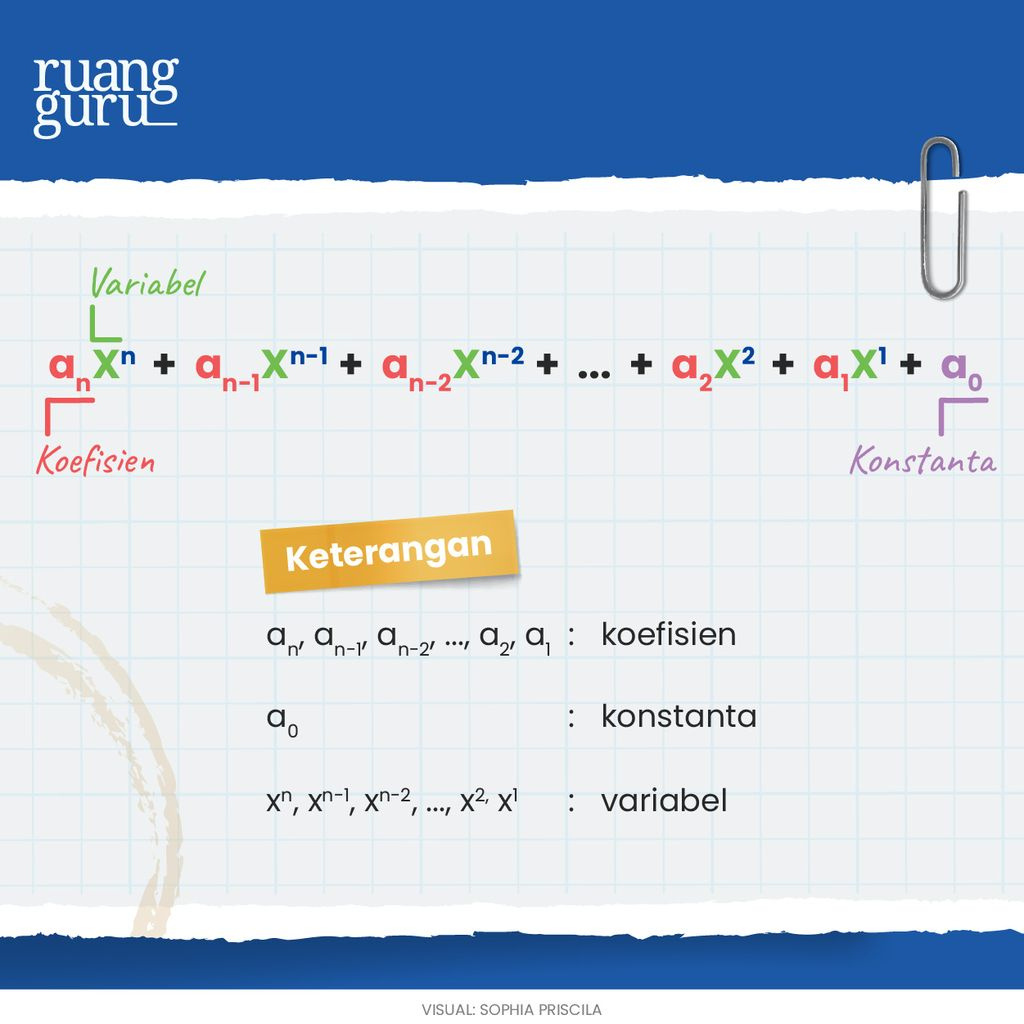
Penjumlahan Suku banyak
Aturan dari penjumlahan suku banyak adalah menjumlahkan suku yang memiliki variabel serta eksponen yang sama atau menjumlahkan suku sejenis. Penjumlahan suku banyak akan menghasilkan suku banyak dengan eksponen yang sama. Misalnya ini:
Contoh Soal:
Jika f(x) = 2x3 + 4x2 + 6x + 8 dan g(x) = 7x2 – 9x – 11maka hasil dari f(x) + g(x)=…
Pembahasan:
f(x) +g(x) = (2x3 + 4x2 + 6x + 8) + (7x2 – 9x – 11)
= 2x3 + (4 + 7)x2 + (6 – 9)x + 8 -11
= 2x3 + 11x2 – 3x – 3
Jadi hasil penjumlahan f(x) dan g(x)adalah 2x3 + 11x2 – 3x – 3
Pengurangan Suku banyak
Pengurangan suku banyak artinya, mengurangkan suku dengan variabel dan eksponen yang sama atau mengubah tanda fungsi yang dikurangi. Sebenarnya, aturan pegurangan sama dengan penjumlahan, letak perbedaanya hanya pada operasinya saja. Tapi, kamu harus teliti untuk tanda plus dan minusnya ya!
Contoh Soal:
Diketahui f(x) = 5x4 + 7x2 – 3x + 5 dan g(x) = 4x4 – 8x3 + 2x + 10, tentukan hasil dari f(x) -g(x)!
Pembahasan:
f(x) – g(x) = (5x4 + 7x2 – 3x + 5) – (4x4 – 8x3 + 2x + 10)
= (5 – 4)x4 – (- 8x3) + 7x2 + (- 3 – 2)x + 5 – 10
= x4 + 8x3 + 7x2 – 5x – 5
Perkalian Suku banyak
Mengalikan satu per satu suku yang ada, hingga memperoleh eksponen yang lebih tinggi atau kita menggunakan sifat distributif. Kalo kamu lupa, sifat distributif itu misalnya kaya gini
Contoh Soal:
Tentukan hasil dari perkalian dua suku banyak ini (2x2 + 6)(x3 – x + 2)!
Pembahasan:
Kamu bisa menggunakan sifat distributif, seperti ini
(2x2)(x3) + (2x2)(-x) + (2x2)(2)+(6)(x3) + (6)(-x)+(6)(2)
= 2x2+3 – 2x2+1 + 4x2+0 + 6x3 – 6x+12
= 2x5 – 2x3 + 4x2 + 6x3 – 6x+12
= 2x5 + (-2+6)x3 + 4x2 – 6x+12
= 2x5 + 4x3 + 4x2 – 6x+12
Pembagian bersusun



Pembagian Horner
Aturan penggunaan metode horner pada operasi pembagian adalah sebagai berikut :
1.Letakkan seluruh koefisien dari derajat tertinggi sampai nol di bagian atas (selalu dimulai dari pangkat tertinggi dan berurutan). Apabila terdapat suku banyak yang tidak ada contohnya 2x4 + 3x2-5x-9 = 0. Maka koefisien untuk pangkat x3 dapat ditulis 0.
2.Letakkan faktor pengali di samping kiri.
3.Baris bawah bagian kiri adalah hasil bagi, sedangkan bagian kanan adalah sisa. Atau dapat ditulis sebagai berikut
:
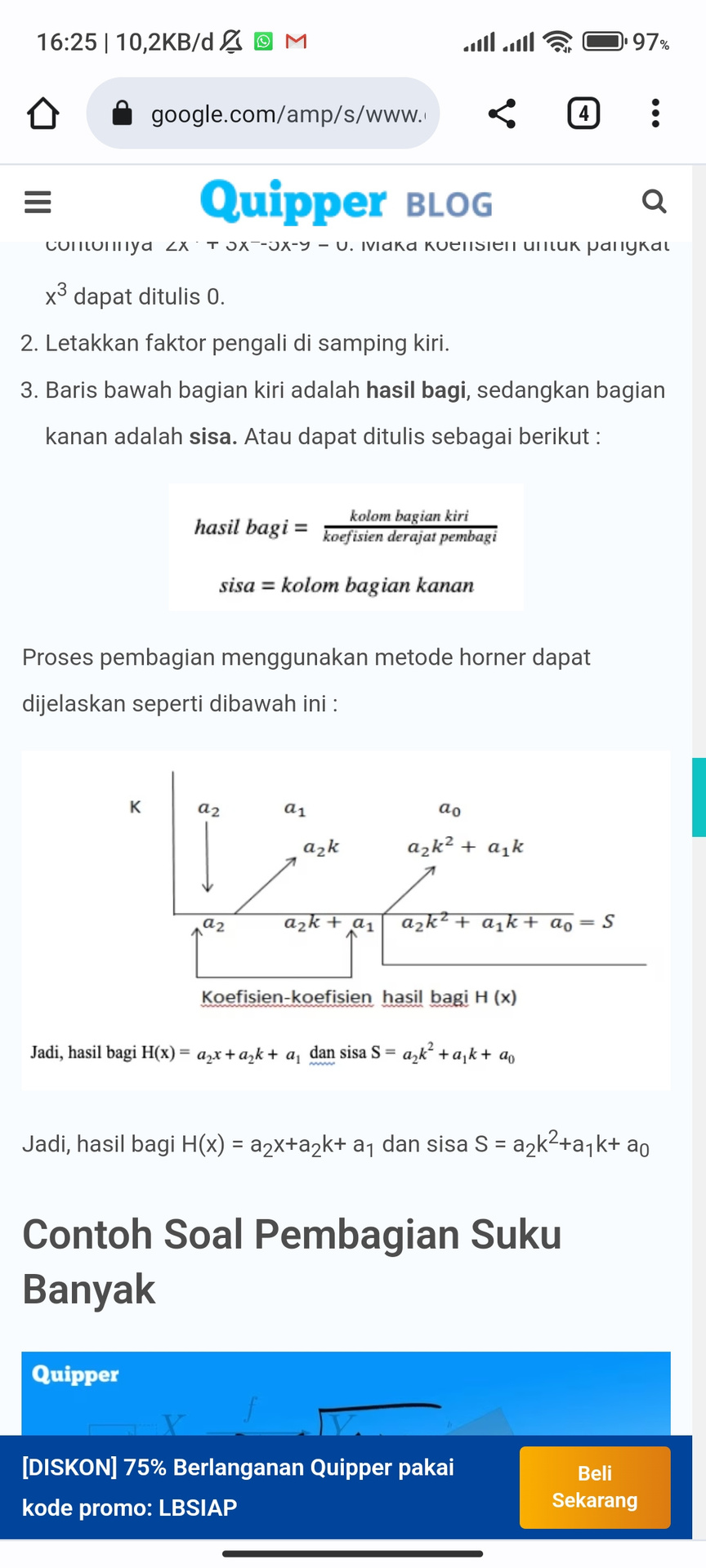
Teorema sisa
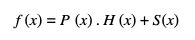
Jika F(x) suku banyak berderajat n dan P(x) adalah pembagi berderajat m, dengan m ≤ n, maka diperoleh :
1.H(x) adalah hasil bagi berderajat (n-m).
2.S(x) adalah sisa pembagian berderajat maksimum (m-1).
Syarat pembagi menggunakan teorema sisa terdapat dengan dua cara yaitu :
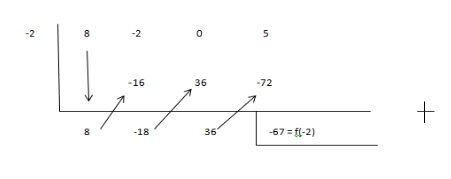
1. Carilah sisa pembagi suku banyak 8x3-2x2+5 dengan (x+2)
a. Dengan cara substitusi
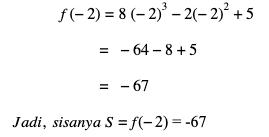
b. Menggunakan skema (bagan) dengan pembagian (x-k)
Teorema faktor
Teorema faktor dapat digunakan untuk menentukan faktor lain atau akar-akar rasional dari sistem persamaan suku banyak menggunakan metode horner. Pada teorema faktor menjelaskan 2 konsep yaitu :
1.Jika P(x) habis dibagi q(x) atau mempunyai sisa nol, maka q(x) adalah faktor dari P(x)
2.Jika P(x) = f(x). g(x) maka f(x) dan g(x) adalah faktor dari P(x).
Contoh soal
1. Jika salah satu akar dari f(x) = x4+ mx3-6x2+7x-6 adalah 2, tentukan akar linear lainnya!
Pembahasan :
Langkah pertama : carilah terlebih dahulu nilai m dengan substitusi polinomial f(2) = 0, karena nilai 2 termasuk akar dari f(x), maka diperoleh :
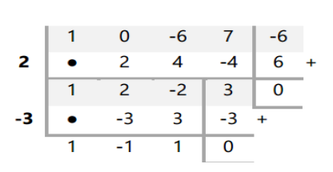
Kemudian gunakan metode horner untuk menentukan faktor atau akarainnya, yaitu :
Sehinga faktor (x) yang lain adalah (x-2), (x+3), dan (x2-x+1). Oleh sebab itu, faktor lain dari akar linearnya adalah -3.
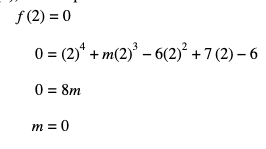
TERIMA KASIH